先日のマンデルブロー集合の10の200乗倍で作成したプログラムがあるので、今回はマンデルブロー集合の様々な地点へ飛び込んだ動画を作ってみました。
前回の記事を見ていない方はそちらからどうぞ:
[フラクタル] マンデルブロー集合 10の200乗倍への挑戦
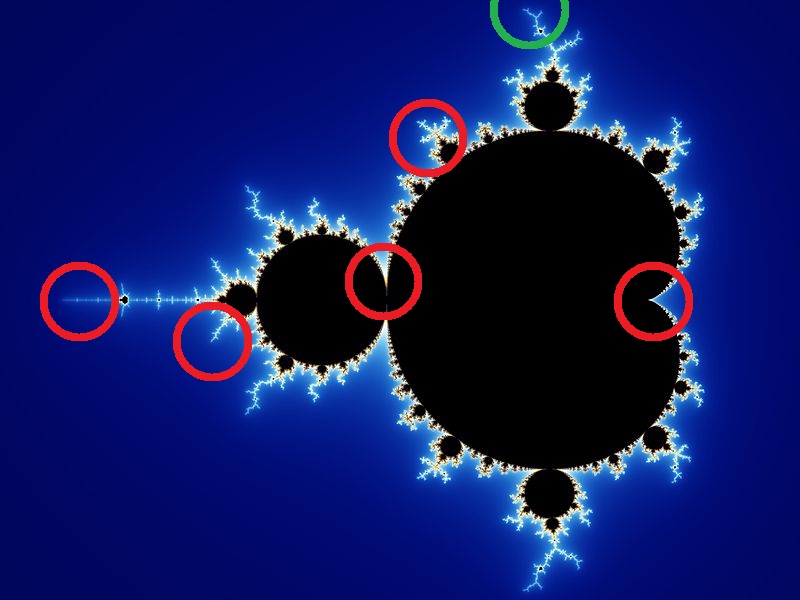
今回訪れる地点は計5箇所です。どの点も拡大していく最中に集合全体と同じ形が現れます。フラクタルらしくて面白いと思います。
具体的には以下の点です。緑は前回の場所。それぞれ個性的な場所だと思います。
この集合はフラクタルなので自己相似の図形ではあるのですが、ただ単純にどこでも同じ形を持っているわけではありません。拡大する場所を変えると景色が一変してしまいます。
肝心の動画はこちら。ニコニコ動画はこちら。
動画の解説
マンデルブロー集合の簡単な解説は前回の記事を見てもらうとして、いろいろと質問に答えておきたいと思います。
- 色はどうやってつけているの?
値が収束する範囲は黒で、発散するところ(だいたい全部)に色をつけています。
前回も書いたように色は値が発散する速度です。拡大するほど境界に近づいて収束の判定が微妙になっていくので、発散するまでより高精度かつ大量の収束計算を行う必要がでてきます。
もっとも色は無限には用意できないので、青→白→黄→赤の循環色で表現しています。色温度の順とかあれこれ考えたのですが、最後は見た目で決めました。
- CPU時間で200時間っていろいろぶっ飛んでいるのでは?
MPI並列化をしているのでコア数分は短縮できるのと、常に保存しながらぶん回していたのでそれほど怖くはありませんでした。
- 収束する先は…?
計算で出したりしているのではなく、目で見て決めています。マンデルブロー集合はフラクタルとはいえほとんどの部分は何もない荒野になっているので、適当な地点を拡大するときは自分で行き先を選んでいかなければなりません。
手順としてははじめにざっくりと計算しながら手作業でざくざく拡大していき、目標地点を決めたらはじめから綺麗に描画し直しています。
ソースコード
読みにくいですが、大事な部分だけ一応置いておきます。
おおよそ以下のようになっています。本当はMPI並列化とアニメーションを保存する部分とでもっと煩雑(分量で3倍程度)になっていますが、以下はその前の段階に試しにざくざく書いてみたものです。(試し書きのままなので多少バグがあるかもしれません。動作は確認しました。)
マウスでクリックして拡大縮小するのでこのまま遊べます。ただし下のコードは精度を後から変えられるようにしていないので、このまま拡大しすぎるとモザイクになるかもしれません。
#include <iostream>
#include <sstream>
#include <vector>
#include <thread>
#include "glut.h"
#include "gmpxx.h"
const int Mx = 200, My = 150;
const double Yratio = My*1.0/Mx;
long long int lMax = 200;
mpf_class ranger(3,65536);
mpf_class br(-2, 65536);
mpf_class bi(-3*0.75*0.5+0.0001, 65536);
void hsvTorgb(double h, double s, double v, double& r, double& g, double& b){
int hi = static_cast<int>(h/60.0) % 6;
double f = h/60.0 - hi;
double p = v*(1.0 - s);
double q = v*(1.0 - f*s);
double t = v*(1 - (1 - f)*s);
switch(hi){
case 0:
r = v; g = t; b = p;
return;
case 1:
r = q; g = v; b = p;
return;
case 2:
r = p; g = v; b = t;
return;
case 3:
r = p; g = q; b = v;
return;
case 4:
r = t; g = p; b = v;
return;
case 5:
r = v; g = p; b = q;
return;
}
}
const long long int converge(const mpf_class& fr, const mpf_class& fi, const long long int maximum){
mpf_class tr(fr), ti(fi), tmp;
mpf_class t1(0, 500), t2(0, 500), t3(0, 500);
int loop;
for(loop = 0; loop < maximum; loop++){ t1 = tr*tr; t2 = ti*ti; t3 = tr*ti; tr = t1-t2+fr; ti = 2.0*t3+fi; if(t1+t2 > 4.0) break;
}
return loop;
}
void display_string(float x, float y, std::string str){
glDisable(GL_TEXTURE_2D);
glColor4f(0.7f,0.8f,0.8f,1.0f);
glRasterPos3f(x, y, -1.0f);
const char* p = str.c_str();
while (*p != '\0') glutBitmapCharacter(GLUT_BITMAP_HELVETICA_10, *p++);
glEnable(GL_TEXTURE_2D);
}
void display_params(){
std::stringstream ss;
ss << lMax << " " << ranger;
display_string(-0.9f, -0.9f, ss.str());
}
void display(){
std::vector<float> tex(Mx*My*3);
//glClear(GL_COLOR_BUFFER_BIT);
mpf_class step(ranger);
step = step/Mx;
auto partialFillTex = [&tex, &step](int ibegin, int iend){
for(int i = ibegin; i < iend; i++){
int col = i*Mx*3;
for(int j = 0; j < Mx; j++){
int tPos = col+3*j;
double r, g, b;
long long int h = converge(br+step*j, bi+step*i, lMax);
if(h == lMax){
r = g = b = 0.0;
}else{
hsvTorgb((h*3)%360, 1.0, 1.0, r, g, b);
}
tex[tPos] = r;
tex[tPos+1] = g;
tex[tPos+2] = b;
}
}
};
const int threadNum = 16;
std::vector<std::thread> threads;
for(int i = 0; i < threadNum; i++){
threads.push_back(std::thread(partialFillTex, i*My/threadNum, (i+1)*My/threadNum));
}
for(int i = 0; i < threadNum; i++){
threads.at(i).join();
}
glTexImage2D(GL_TEXTURE_2D, 0, GL_RGB, Mx, My, 0, GL_RGB, GL_FLOAT, &(tex[0]));
glColor3f(1.0f, 1.0f, 1.0f);
glBegin(GL_POLYGON);
glTexCoord2f(0, 0); glVertex2f(-1.0f, 1.0f);
glTexCoord2f(0, 1); glVertex2f(-1.0f, -1.0f);
glTexCoord2f(1, 1); glVertex2f(1.0f, -1.0f);
glTexCoord2f(1, 0); glVertex2f(1.0f, 1.0f);
glEnd();
display_params();
glutSwapBuffers();
}
void keyboard(unsigned char key, int x, int y){
switch(key){
case 'q':
lMax *= 2;
break;
case 'w':
lMax /= 2;
break;
}
}
void mouse(int button, int state, int x, int y){
if(state != GLUT_DOWN) return;
double rx = static_cast<double>(x) / static_cast<double>(Mx);
double ry = static_cast<double>(y) / static_cast<double>(My);
if(button == GLUT_LEFT_BUTTON){
//br.set_prec(br.get_prec()+1);
//bi.set_prec(bi.get_prec()+1);
//ranger.set_prec(ranger.get_prec()+1);
br = br + 0.75 * rx * ranger;
bi = bi + 0.75 * ry * Yratio * ranger;
ranger = 0.25 * ranger;
}else if(button == GLUT_RIGHT_BUTTON){
br = br - rx * ranger;
bi = bi - ry * Yratio * ranger;
ranger = 2.0 * ranger;
}
glutPostRedisplay();
}
int main(int argc, char** argv){
glutInitWindowPosition(100, 100);
glutInitWindowSize(Mx, My);
glutInit(&argc, argv);
glutCreateWindow("Hoge");
glutInitDisplayMode(GLUT_RGBA | GLUT_DOUBLE);
glutDisplayFunc(display);
glutKeyboardFunc(keyboard);
glutMouseFunc(mouse);
glClearColor(0.0f, 0.0f, 1.0f, 1.0f);
glEnable(GL_TEXTURE_2D);
GLuint texture;
glGenTextures(1, &texture);
glBindTexture(GL_TEXTURE_2D, texture);
glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_MAG_FILTER, GL_LINEAR);
glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_MIN_FILTER, GL_LINEAR);
glutMainLoop();
glDeleteTextures(1, &texture);
return 0;
}
色をわざわざHSV色空間で用意したりしていますね。あとマルチスレッド並列化(16並列)がなされています。
コンパイルにはライブラリとしてGLUT(今回使用したのはfreeglut)とGMPが必要です。
一番大事なのは関数convergeです。これを各点についてひたすら実行して、収束するか、あるいはどれくらいの勢いで発散するかを求めています。
描画/UI周りで大したことをしていないのにこれだけ記述が必要になるのはC/C++らしいような気もします。もっとも今回は計算速度重視なので、それでもC/C++で全部書いてしまったほうが楽だと思いますが。
余談ですが、今回のような「各画素について~」という作業では並列化の効率が非常に良くなります。グラフィック周りの計算ではその性質が強いためGPUのような並列化がとても有効ですが、科学技術計算などでは必ずしもそこまで簡単にはなってくれません。物理現象を記述する際には隣接する要素がどうのこうの、という話が必要になってきて、そうなると今度はボトルネックが通信の側に偏ってくるのです。もどかしいですね。
マンデルブロー集合の名前にもなっているブノワ・マンデルブローという方は、フラクタルという概念そのものを提案したとても有名な人です。先日(2010年10月)に亡くなったというニュースが出たときには、私の知り合いの中でも驚きの声が上がりました。
この方は純粋な数学だけでなく、流体などの自然科学、情報理論、経済学にわたる多くの分野で論文を発表した多彩な人です。マンデルブローさんにとっては、自分の中ではいろいろな現象をある視点から統一的に見渡すことができたのでしょう。


ピンバック: [フラクタル] マンデルブロー集合 10の200乗倍への挑戦 | ぞうさんの何でもノート